Distance between two parallel lines

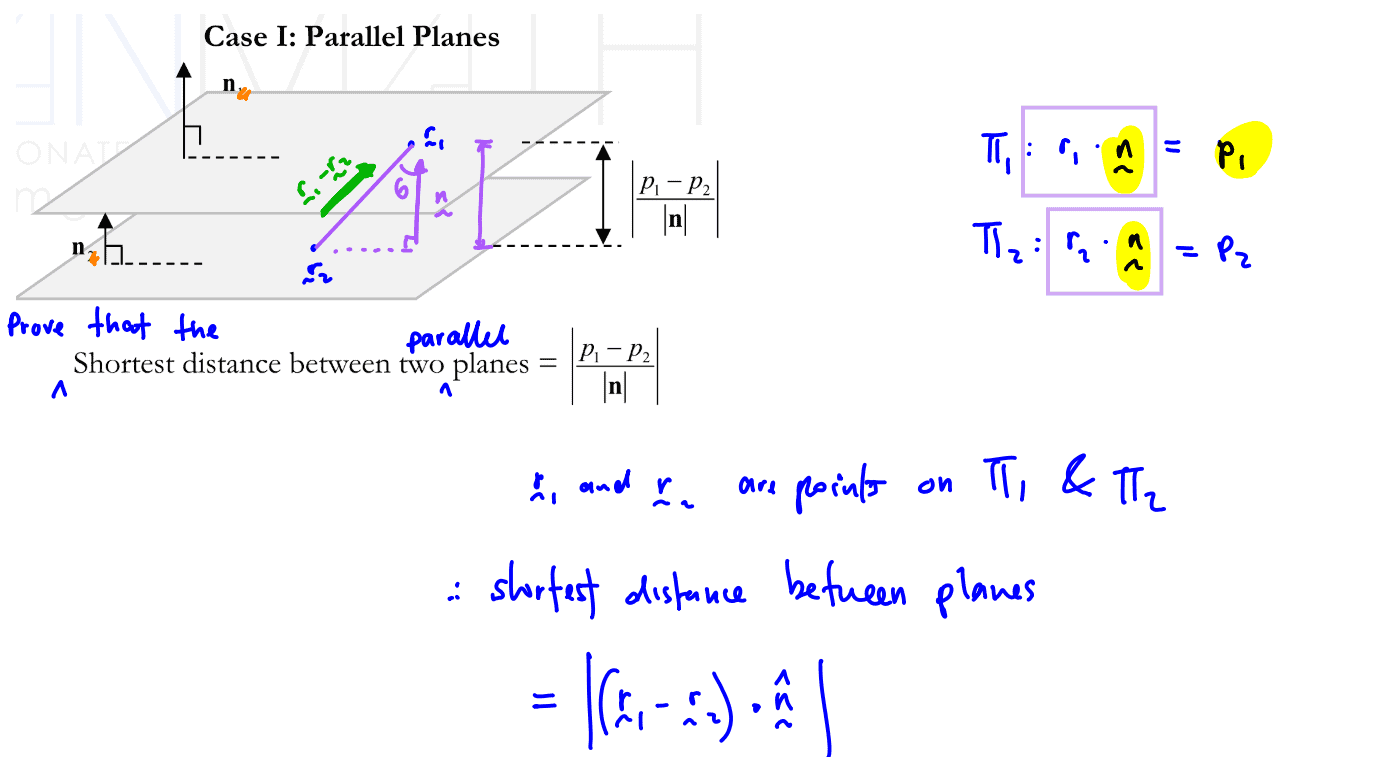
The distance between two parallel lines in the plane is the minimum distance between any two points.

Formula and proof

Because the lines are parallel, the perpendicular distance between them is a constant, so it does not matter which point is chosen to measure the distance. Given the equations of two non-vertical parallel lines

${\displaystyle y=mx b_{1}\,}$

${\displaystyle y=mx b_{2}\,,}$

the distance between the two lines is the distance between the two intersection points of these lines with the perpendicular line

${\displaystyle y=-x/m\,.}$

This distance can be found by first solving the linear systems

${\displaystyle {\begin{cases}y=mx b_{1}\\y=-x/m\,,\end{cases}}}$

and

${\displaystyle {\begin{cases}y=mx b_{2}\\y=-x/m\,,\end{cases}}}$

to get the coordinates of the intersection points. The solutions to the linear systems are the points

${\displaystyle \left(x_{1},y_{1}\right)\ =\left({\frac {-b_{1}m}{m^{2} 1}},{\frac {b_{1}}{m^{2} 1}}\right)\,,}$

and

${\displaystyle \left(x_{2},y_{2}\right)\ =\left({\frac {-b_{2}m}{m^{2} 1}},{\frac {b_{2}}{m^{2} 1}}\right)\,.}$

The distance between the points is

${\displaystyle d={\sqrt {\left({\frac {b_{1}m-b_{2}m}{m^{2} 1}}\right)^{2} \left({\frac {b_{2}-b_{1}}{m^{2} 1}}\right)^{2}}}\,,}$

which reduces to

${\displaystyle d={\frac {|b_{2}-b_{1}|}{\sqrt {m^{2} 1}}}\,.}$

When the lines are given by

${\displaystyle ax by c_{1}=0\,}$

${\displaystyle ax by c_{2}=0,\,}$

the distance between them can be expressed as

${\displaystyle d={\frac {|c_{2}-c_{1}|}{\sqrt {a^{2} b^{2}}}}.}$

See also

• Distance from a point to a line

References

• Abstand In: Schülerduden – Mathematik II. Bibliographisches Institut & F. A. Brockhaus, 2004, ISBN 3-411-04275-3, pp. 17-19 (German)
• Hardt Krämer, Rolf Höwelmann, Ingo Klemisch: Analytische Geometrie und Lineare Akgebra. Diesterweg, 1988, ISBN 3-425-05301-9, p. 298 (German)

External links

• Florian Modler: Vektorprodukte, Abstandsaufgaben, Lagebeziehungen, Winkelberechnung – Wann welche Formel?, pp. 44-59 (German)
• A. J. Hobson: “JUST THE MATHS” - UNIT NUMBER 8.5 - VECTORS 5 (Vector equations of straight lines), pp. 8-9